本セッションでは、C/C++ 言語により局面を表すデータ構造にビットボード(bitboard)を用いた 4x4 オセロ完全解析プログラムについて解説し、 その解析結果について報告する。
[1] オセロのルール自体は古くから存在した。 「緑の盤面に黒い線を引いて8x8の升目を作り、白黒の丸い石を用いる」というのが登録商標になっている。
目次:
- 4x4 オセロ
- 完全解析
- ゲーム木探索
- ビットボード(データ構造+アルゴリズム)(17:05〜17:35)
- 局面表現
- 石数を数える
- 石を返す
- 着手可能判定、反転パターン取得
- 空欄に対する処理
- ネガマックス
- トランスポジションテーブル
- 完全解析結果
4x4 オセロ
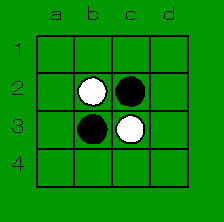
4x4 オセロの初期状態を上図に示す。黒番から始める。
- 空きは12個なので、最長12手で終わる。
- 初手は、a2, b1, c4, d3 の4通りあるが、対称形なので(数学的には)どれも同じである。
オセロのルール
- 黒白交互に打つ
- 相手の石を縦横斜めに挟む位置にのみ着手可能
- 挟んだ石は自分の色になる
- 着手可能箇所があれば、着手しなくてはいけない
- 着手不可能な場合はパス
- 双方着手不可能になると終局
- 終局時に石数の多い方が勝ち
- 試合では石差をポイントとすることが多い
4x4 オセロ 可能な局面数の見積もり
各升目の状態は、黒・白・空白の3状態なので、可能な局面数の上限は 3^16 = 43,046,721
回転・対称形を取り除くとその数分の1になる。
この中には初期局面から到達不可能な局面も多数存在する。
初手1通り、それ以降は4通りの着手箇所があり、最後の3個空きからは空き個数の着手可能箇所があるとすれば、 末端局面数は 1*4*4*4*4*4*4*4*4*3*2*1 = 393,216 となる。
参考までに、8x8オセロの末端局面数は約10^60と言われている。ちなみにチェスは約10^120, 将棋は約10^220、囲碁は10^360 と言われている。
完全解析
完全解析とは、初期局面からゲームルールに従って到達可能な全局面を調査し、双方が常に最善手を打つと仮定して、
それら全ての勝ち負けを決定することである。
オセロの場合は勝ち負けだけなく石差が重要なので、石差を計算する。
例えば、下図の2手目(白番)の局面は白は、d2, b4, d4 に着手可能で、その後双方最善手を打ったとすると、
石差は(白から見て) -8、-9、+8 となるので、2手目の最善手は d4 で白の8石勝ちとなる。
a b c d ┏━┯━┯━┯━┓ 1┃ │ │ │ ┃ ┠─┼─┼─┼─┨ 2┃ │○│●│-8┃ ┠─┼─┼─┼─┨ 3┃ │●│●│●┃ ┠─┼─┼─┼─┨ 4┃ │-9│ │+8┃ ┗━┷━┷━┷━┛
ゲーム木探索
初期状態を根(root)とし、可能な着手を枝(branch)とすると、
ゲーム全体をひとつの大きな木で表すことができる。この木のことをゲーム木(game tree)と呼ぶ。
それぞれの局面はノード(node)と呼ばれ、
終局局面は葉/末端/終端ノード(leaf/teminal node)と呼ばれる。
root
┏━┯━┯━┯━┓
┃ │ │ │ ┃
┠─┼─┼─┼─┨
┃ │○│●│ ┃
┠─┼─┼─┼─┨
┃ │●│○│ ┃
┠─┼─┼─┼─┨
┃ │ │ │ ┃
┗━┷━┷━┷━┛
│
├──────────────────────────┬────────┬────────┐
│ │ │ │
┏━┯━┯━┯━┓ ┏━┯━┯━┯━┓┏━┯━┯━┯━┓┏━┯━┯━┯━┓
┃ │ │ │ ┃ ┃ │ │ │ ┃┃ │ │ │ ┃┃ │●│ │ ┃
┠─┼─┼─┼─┨ ┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃ │○│●│ ┃ ┃ │○│●│ ┃┃●│●│●│ ┃┃ │●│●│ ┃
┠─┼─┼─┼─┨ ┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃ │●│●│●┃ ┃ │●│●│ ┃┃ │●│○│ ┃┃ │●│○│ ┃
┠─┼─┼─┼─┨ ┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃ │ │ │ ┃ ┃ │ │●│ ┃┃ │ │ │ ┃┃ │ │ │ ┃
┗━┷━┷━┷━┛ ┗━┷━┷━┷━┛┗━┷━┷━┷━┛┗━┷━┷━┷━┛
│ : : :
│
├────────┬────────┐
│ │ │
┏━┯━┯━┯━┓┏━┯━┯━┯━┓┏━┯━┯━┯━┓
┃ │ │ │ ┃┃ │ │ │ ┃┃ │ │ │ ┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃ │○│○│○┃┃ │○│●│ ┃┃ │○│●│ ┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃ │●│●│●┃┃ │○│●│●┃┃ │●│○│●┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃ │ │ │ ┃┃ │○│ │ ┃┃ │ │ │○┃
┗━┷━┷━┷━┛┗━┷━┷━┷━┛┗━┷━┷━┷━┛
: : :
:
:
:
┏━┯━┯━┯━┓
┃ │●│●│●┃
┠─┼─┼─┼─┨
┃ │●│●│●┃
┠─┼─┼─┼─┨
┃ │●│●│●┃
┠─┼─┼─┼─┨
┃●│○│○│○┃
┗━┷━┷━┷━┛
│
├─────────────────┐
│ │
┏━┯━┯━┯━┓ ┏━┯━┯━┯━┓
┃○│●│●│●┃ ┃ │●│●│●┃
┠─┼─┼─┼─┨ ┠─┼─┼─┼─┨
┃ │○│●│●┃ ┃○│●│●│●┃
┠─┼─┼─┼─┨ ┠─┼─┼─┼─┨
┃ │●│○│●┃ ┃ │○│●│●┃
┠─┼─┼─┼─┨ ┠─┼─┼─┼─┨
┃●│○│○│○┃ ┃●│○│○│○┃
┗━┷━┷━┷━┛ ┗━┷━┷━┷━┛
│ │
├────────┐ │
│ │ │
┏━┯━┯━┯━┓┏━┯━┯━┯━┓┏━┯━┯━┯━┓
┃○│●│●│●┃┃○│●│●│●┃┃ │●│●│●┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃●│●│●│●┃┃ │●│●│●┃┃○│●│●│●┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃ │●│○│●┃┃●│●│○│●┃┃●│●│●│●┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃●│○│○│○┃┃●│○│○│○┃┃●│○│○│○┃
┗━┷━┷━┷━┛┗━┷━┷━┷━┛┗━┷━┷━┷━┛
│ │ │
┏━┯━┯━┯━┓┏━┯━┯━┯━┓┏━┯━┯━┯━┓
┃○│●│●│●┃┃○│●│●│●┃┃○│●│●│●┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃○│●│●│●┃┃○│●│●│●┃┃○│○│●│●┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃○│○│○│●┃┃●│○│○│●┃┃●│●│○│●┃
┠─┼─┼─┼─┨┠─┼─┼─┼─┨┠─┼─┼─┼─┨
┃●│○│○│○┃┃●│○│○│○┃┃●│○│○│○┃
┗━┷━┷━┷━┛┗━┷━┷━┷━┛┗━┷━┷━┷━┛
黒±0 黒+2 黒+2
初期状態から始めて、局面を生成しつつゲーム木を調査することを、ゲーム木探索と呼ぶ。
ゲーム木探索に関する項目としては以下のようなものがある。
- ミニマックス評価
- アルファベータ法
- 枝刈り(前向き・後ろ向き)
- 深さ優先探索
- 幅優先探索
- 反復深化
- トランスポジション テーブル
- 対称形除去
- 後退解析
時間がないので説明は省略。自分で調べてね。;^p
ビットボード(bitboard)
(17:05〜17:35)ビットボードによる局面の表現
ビットボードとは盤面の黒石・白石の状態をそれぞれビット値で表すデータ構造である:ushort black, white;
石がある部分は1、無い部分は0をビット値とする。
4x4 オセロは16マスなので、16ビット整数(ushort)でひとつの種類の石を表現できる。
初期局面は、黒石:0x0240、白石:0x0420 と表現できる(2進数では、0000 0010 0100 0000、0000 0100 0010 0000)。

盤面は2次元なので2次元配列で局面を表現可能:char board[4][4];
2次元配列はアドレス計算に時間がかかるので、通常は番人を用いた1次元配列を使用することが多い:
char board[5*6+1];
これらに比べてビットボード(bitboard)データ構造は、使用メモリ量・処理速度の両面で効率的に局面を表現できる。
char board[4][4]; は16バイト、
char board[5*6+1];は31バイトものメモリが必要だが、
ビットボードであれば4バイトですむ。
32ビットレジスタ1個にパックすることも可能。
ビットボードを用いると、以下の点で処理速度が向上する。
- 各ビットを同時並行的に処理することが可能(O(N) → O(logN)〜O(1))
- シフトと算術論理演算により条件分岐を行わない記述が可能
- 白黒反転など処理が簡単になる場合が多い
以下、ビットボードを4x4オセロ完全解析に用いたアルゴリズムを解説する。
ビットボードの起源(wikipedia より引用):
The bitboard method for holding a board game appears to have been invented in the mid 1950's, by Arthur Samuel and was used in his checkers program. The method was published in 1959 as "Some Studies in Machine Learning Using the Game of Checkers" in the IBM Journal of Research and Development.
For the more complicated game of chess, it appears the method was independently rediscovered later by the Kaissa team in the Soviet Union in the late 1960s, although not publicly documented, and again by the authors of the U.S. Northwestern University program "Chess" in the early 1970s, and documented in 1977 in "Chess Skill in Man and Machine".
空白があるかどうかの判定
空白が無くなった場合、双方着手することができないので終局となる。
空白があるかどうかは、黒石 black, 白石 white の算術論理和が 0xffff かどうかで判定できる。
// 盤面に空欄が無い場合に true を返す
inline bool isBoardFull(ushort black, ushort white)
{
return !~(black | white);
}
上記処理の処理時間は O(1) である。ループを用いる場合は O(N) である。
石数の数え上げ
オセロの勝敗は終局時の石数差で決まるので、石数を数える処理は重要である。
素直にビット数分ループを行い、ビットを数えるプログラムは以下のようになる。処理時間は O(N)
// 立っているビット数を数える。ループを用いる版(処理時間は O(N))
int numOfBits(ushort bb)
{
int count = 0;
for(ushort mask = 0x8000; mask != 0; mask >>= 1)
if( (bb & mask) != 0 )
++count;
return count;
}
下図の様に最初に隣り合う2ビットごとにビット数を数え、次は4ビット、その次は8ビットと増やしいくことで 値が1のビット数をカウントすることができる。 処理時間は O(logN) となる。
┌─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┐ │0│0│0│1│1│0│1│1│0│0│1│1│0│0│0│1│ 1をカウントするデータ ├─┴─┼─┴─┼─┴─┼─┴─┼─┴─┼─┴─┼─┴─┼─┴─┤ │ 0│ 1│ 1│ 2│ 0│ 2│ 0│ 1│ 隣り合う2ビットごとにカウント ├───┴───┼───┴───┼───┴───┼───┴───┤ │ 1│ 3│ 2│ 1│ 4ビットごとにカウント ├───────┴───────┼───────┴───────┤ │ 4│ 3│ 8ビットごとにカウント ├───────────────┴───────────────┤ │ 7│ 16ビット分カウント └───────────────────────────────┘
ビット数が少ない場合は、ループを用いる版と処理速度に大差はないが、ビット数が多くなるほど有利になる。
// 立っているビット数を数える。分割統治法を用いる版(処理時間は O(logN))
ushort numOfBits(ushort bits)
{
bits = (bits & 0x5555) + (bits >> 1 & 0x5555); // 2bitごとに計算
bits = (bits & 0x3333) + (bits >> 2 & 0x3333); // 4bitごとに計算
bits = (bits & 0x0f0f) + (bits >> 4 & 0x0f0f); // 8bitごとに計算
return (bits & 0x00ff) + (bits >> 8 & 0x00ff); // 16ビット分を計算
}
NB(b) = b - b/2 - b/4 ... なので、最初の行は以下のように書き換えた方が命令数を少なくできる。
また、8ビットの場合の最大値は8であり4ビットに収まるので、最後の16ビット分の計算はマスク計算をひとつ省略できる。
// 立っているビット数を数える。分割統治法を用いる版(処理時間は O(logN))少し最適化
ushort numOfBits(ushort bits)
{
bits = bits - (bits >> 1 & 0x5555);
//bits = (bits & 0x5555) + (bits >> 1 & 0x5555);
bits = (bits & 0x3333) + (bits >> 2 & 0x3333);
bits = (bits & 0x0f0f) + (bits >> 4 & 0x0f0f);
return (bits + (bits >> 8)) & 0x001f;
//return (bits & 0x00ff) + (bits >> 8 & 0x00ff);
}
※ 2bit の場合の証明:
b = b1*2 + b0
b - b/2 = (b1 *2 + b0) - b1 = b1 + b0
証明終わり。bit数が3以上の場合も同様。
この関数を使って白石・黒石両方の数を数えるには関数を2回呼ぶ必要があるが、 両方の状態を 32ビットにパックすれば、より少ない時間でそれぞれの個数を数え上げることができる。
// 白石・黒石の立っているビット数を同時に数える。
void numOfBits(ushort &b, ushort &w)
{
uint bits = (b << 16) | w;
bits = bits - (bits >> 1 & 0x55555555);
//bits = (bits & 0x55555555) + (bits >> 1 & 0x55555555);
bits = (bits & 0x33333333) + (bits >> 2 & 0x33333333);
bits = (bits & 0x0f0f0f0f) + (bits >> 4 & 0x0f0f0f0f);
bits = (bits & 0x00ff00ff) + (bits >> 8 & 0x00ff00ff);
b = (ushort)(bits >> 16);
w = (ushort)bits;
}
すべての空欄に対する処理
普通にループで書くと以下のようになる。ループ回数は常に16回となる。
ushort space = ~(black | white); // 空欄の部分だけビットを立てる
for(ushort p = 0x8000; p != 0; p >>= 1) { // 各ビットについて
if( (p & space) == 0 ) continue; // 空欄でなければ次のビットへ
// すべての空欄に対する処理
.....
}
-x = ~x + 1 なので、下図の様に x & -x で一番右のビット1だけを取り出すことができる(x が0ときは0を返す)。
┌─────────┐
x:│bb…b100…0│
├─────────┤
~x:│rr…r011…1│
├─────────┤
-x:│rr…r100…0│
├─────────┤
x & -x:│00…0100…0│
└─────────┘
この演算を使えば、すべての空欄に対する処理は以下のように記述できる。ループは空欄の数だけ回る。
ushort space = ~(black | white); // 空欄の部分だけビットを立てる
while( space != 0 ) {
ushort p = space & -space; // 一番右のビットのみ取り出す
// すべての空欄に対する処理
.....
space ^= p; // 一番右のビットをOFFにする
}
石を反転する処理
黒石を置く位置を p、それにより反転するパターンを rev とすれば、
黒石を置いて白石を反転させる処理は以下のように記述できる。
ex-or で演算しているので、この処理は可逆的で、2回コールすると盤面の状態が元に戻る。
inline void doPut( ushort &black, // 黒石
ushort &white, // 白石
ushort p, // 黒石を置く位置
ushort rev) // 反転するビットパターン(計算方法は次節参照)
{
black ^= p | rev;
white ^= rev;
}
反転する石を計算
前節で使用した、反転パターンを求める処理。
ビットボードではシフトと論理演算を用いることにより、すべてのビットについて同時並行的に、
条件にマッチするビットを求めることができる。
たとえば、盤面で白黒の順に並んでいる部分を求めたい場合は、white & (black << 1) & 0xeeee とすればよい。
0xeeee は盤面の右端と左端がつながることを防ぐマスクビットである。
a b c d
┏━┯━┯━┯━┓
1┃ │○│ │ ┃ 0000
┠─┼─┼─┼─┨
2┃○│○│●│○┃ → 0100
┠─┼─┼─┼─┨
3┃●│○│○│●┃ 0010
┠─┼─┼─┼─┨
4┃ │ │ │ ┃ 0000
┗━┷━┷━┷━┛
空・白・黒 と並んでいる場合の反転パターンを得るには、p を空白位置を表す値とするとき、
(p>>1) & white & (black<<1) & 0xeeee とするとよい。
同様に、空・白・白・黒 の最初の白のパターンは (p>>1) & white & (white<<1) & (black<<2) & 0xeeee、
2番目の白の部分は (p>>2) & (white>>1) & white & (black<<1) & 0xeeee となる。
これらの論理和を取ったものが、反転パターンとなる。
ushort get_rev(ushort b, ushort w, ushort p)
{
if( ((b | w) & p) != 0 ) return 0; // p が空白ではない場合
ushort rev = 0; // 反転パターン
const ushort wh = w & 0x6666; // 水平方向用マスク
// 右方向に返る石をチェック
rev |= (p >> 1) & wh & ((b << 1) | ((wh & (b << 1)) << 1)); // 隣の石
rev |= (p >> 2) & (wh >> 1) & wh & (b << 1); // もう一個先の石
// 左方向に返る石をチェック
rev |= (p << 1) & wh & ((b >> 1) | ((wh & (b >> 1)) >> 1)); // 隣の石
rev |= (p << 2) & (wh << 1) & wh & (b >> 1); // もう一個先の石
..... // 他の方向についても同様に処理
return rev;
}
あらかじめ8方向について着手可能箇所を求めておき、各空白については単純な論理演算だけにするという方法もある。
深さ優先探索
int negaMax(ushort black, ushort white)
{
if( 末端局面 )
return numOfBits(black) - numOfBits(white);
int maxVal = INT_MIN;
foreach(p すべての空欄) {
ushort rev = get_rev(black, white, p); // 反転パターン取得
if( rev != 0 ) { // 石が返る場合
doPut(black, white, p, rev); // 石を返す
int v = -negaMax(white, black); // 白黒反転して自分自身を再帰コール
if( v > maxVal ) max = v;
doPut(black, white, p, rev); // 反転した石を戻す
}
}
return maxVal;
}
自分自身をコールする部分は以下のように最適化することもできる。
.....
if( rev != 0 ) { // 石が返る場合
// 白黒反転して自分自身を再帰コール
int v = -negaMax(white ^ rev, black ^ rev ^ p);
if( v > maxVal ) max = v;
}
.....
トランスポジションテーブル
ある局面から、着手A, B, C と 着手C, B, A の様に、異なる手順で同一局面になる場合がある。 このような場合に、同一局面を再度探索しないよう、局面をトランスポジションテーブル(置換表)に登録して回避する。
将棋やチェスの場合は、コマの種類、位置に乱数を割り当て、それらの排他的論理和をハッシュキーとすることが多いが、 4x4オセロでビットボードを用いる場合、32ビット数値で局面を表現できるので、 32ビット数値をそのままハッシュキーに用いることができる。
本稿では下リストの様に boost::unordered_map を利用した。局面の登録・検索は同クラスのメソッド・演算子を利用する。
局面は (black<<16) | white をキーとし、手番は黒番固定とする。
同一局面の白番は白黒を入れ替え((white<<16) | black がキー)て登録する。
boost::unordered_map<uint, char> g_tpTable; // 局面→石差 トランスポジションテーブル
g_tpTable[makeUint(black, white)] = v; // 局面・石差を登録
g_tpTable.find(makeUint(black, white)) // 局面登録チェック
8つの対称形全てを計算し、値が最も小さいものをキーとすることで対称形を除去することができる。
本稿では1手目をd3固定にしたことで大部分の対称形を排除したので、
トランスポジションテーブルによる対称形除去処理は行わなかった。
int negaMax(ushort black, ushort white)
{
if( トランスポジションテーブルに登録されている )
return 登録されている値;
if( 末端局面 ) {
int v = numOfBits(black) - numOfBits(white);
黒番・白番両方で局面登録(v);
return v;
}
int maxVal = INT_MIN;
foreach(p すべての空欄) {
ushort rev = get_rev(black, white, p); // 反転パターン取得
if( rev != 0 ) { // 石が返る場合
// 白黒反転して自分自身を再帰コール
int v = -negaMax(white ^ rev, black ^ rev ^ p);
if( v > maxVal ) max = v;
}
}
黒番で局面登録(maxVal);
return maxVal;
}
※ 本稿のプログラムリストでは煩雑になるのを避けるためにパスの処理を省いているので注意
完全解析結果
(17:35〜)本稿で説明したビットボードを用いたプログラムにより4x4オセロ完全解析を行った結果(の一部)を以下に示す。
解析結果は、2手目に角を取る斜め定石が最善で、白8石勝ちであった。
a b c d ┏━┯━┯━┯━┓ 1┃ │ │ │ ┃ ┠─┼─┼─┼─┨ 2┃ │○│●│-8┃ ┠─┼─┼─┼─┨ 3┃ │●│●│●┃ ┠─┼─┼─┼─┨ 4┃ │-9│ │+8┃ ┗━┷━┷━┷━┛
斜め定石の場合の双方最善の進行を以下に示す。
・-14 ・ ・ ・ ・ ・ ・ -8 ・ ・ ・ ● 4 -4 -4 ● ・ ・ ・ ● -2 8 ・ -14 ○ ● ・ → ・ ○ ● 8 → -14 ○ ● ・ → ・ ● ● 8 → ・ ● ● ○ → -2 ● ● ○ → ・ ● ○ ● ・ ● ● ● -12 ○ ● ● ・ ○ ● ● ・ ○ ○ ○ 6 ● ○ ○ ・ ・ -8 ○ ・ 8 ● ○ -9 ○ ○ ○ ・ ○ ○ ○ -8 ○ ○ ○ ● ○ ○ ○ ● ・ ○ -8 ● 8 ○ ● ● ○ ○ ● ・ ● ○ ○ → 0 ● ● ○ → ・ ○ ○ ○ ・ ● ○ ○ -2 ● ○ ○ ・ ○ ○ ○ ● ○ ○ ○ ● ○ ○ ○ ● ○ ○ ○ 白8石勝ち
- 序盤?で角を取るのは 4x4 オセロでも有利なようだ。
- 7手目黒a3の局面までは、通常オセロの斜め定石→バッファロー→大量取定石と同じ進行。
- 8手目:a3に打って種を作り、右上隅を固めたくなるが、a3->a2->d1 で黒パスになってしまい、 手どまりを打てなくなる。
- 初中級者は無意味に角を取りたがるが、わざと角を取らせて確定石を稼ぐという有段者的打ち回し。
- 最後は2個空きの終局。
縦定石の場合の双方最善の進行を以下に示す。
8 ・ ・ ・ ・-11 ・ -9 ・ ・ ・ -2 ・ ・ ・ -2 ・-15 ・ -9 ・ 9 -2 ○ 9 ○ ● ・ → ● ● ● -9 → ● ● ● ○ → ● ● ● ○ → ● ● ● ○ → ● ● ○ ○ → 2 ○ ● ● ・ ○ ● ● 12 ○ ○ ● 12 ○ ○ ● ・ ○ ● ● -4 ○ ● ● 8 ○ ・ ・ ・ ○ ・ ・ -8 ○ -8 9 -8 ○ -8 9 ・ ○ ・ ● ・ ○ -2 ● ・ ● ・ ○ ・ ● ・ ○ ・ ● ・ ○ ・ ● ・ ○ ・ ● ・ ○ ● ● ● ○ → ● ● ● ○ → ● ● ● ○ → ● ● ● ○ → ● ● ● ○ ・ ○ ● ● 2 ○ ● ● ・ ● ● ● ・ ● ● ● ・ ● ● ● ・ ○ ・ ● 9 ○ 2 ● ● ○ ・ ● ● ○ 9 ● ● ● ● ● 黒9石勝ち
- 3手目はいろいろな手があるが、a2の羊定石が最善だった。a1トラ定石、a4野ウサギ定石はそれに次ぐ手。 筆者の愛用するうさぎ定石は7石損の手だった。
- 8手目b1は読みきらないと打てない手。
- 最後3連打で3箇所空きの終局は見事。
並び定石の場合の双方最善の進行を以下に示す。
-2 -8-12 8 ・ ・ ・ ● ・-10 ・ ● ・ ・ ・ ● 8 ・ ・ ● ●-10 -8 ● ・ ○ ○ ○ ・ ○ ● ● → -4 ○ ● ● → ・ ○ ● ● → -2 ○ ● ● → ・ ● ● ● → ・ ● ● ● → ・ ● ● ● ・ ● ○ ● ・ ● ● ● 0 ○ ● ● ・ ○ ● ● ・ ・ ・ ・ ・-14 ・ -8 ・ 8 8 ○ ・ -8 ● ○ 2 ○ ○ ○ ・ ○ ○ ○ ● 8 ○ ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ・ ● ○ ● → ・ ● ● ● → ・ ● ● ● → -8 ● ● ● → ○ ● ● ● → ○ ● ● ● 2 ○ ○ ● ・ ○ ○ ● 8 ○ ○ ● ● ● ● ● ● ○ ● ● ● ● ● ● 0 ○ ○ ○ ・ ○ ○ ○ 6 ○ ○ ○ ・ ○ ○ ○ 8 ○ ○ ○ ● ○ ○ ○ 黒8石勝ち
- 10手目角を取らずにCに打つのはよくある手筋。c3の石が黒になるぶん得。
(トランスポジションテーブルを使用した場合の)末端局面数は 15,015、処理時間は 0.047秒だった。
※ 環境:ウルフデール3GHz, WinXP, VC9
終わりに
4x4 オセロ完全解析を行うための、ビットボードデータ構造・アルゴリズムについて解説した。
状態数が限られている場合は、状態をビットで表すことで、演算を並列化し、高速化できる場合があるので試してみるといいだろう。
懇親会にてエキジビションマッチを行います。
オセロ 弐段の筆者がお相手しますので、オセロの腕に自信がある方はぜひ挑戦してみてください。