「関数電卓」アプリを開発しリリースした。
三角関数・指数関数などを数式通りに入力し、計算結果を表示することができるのはもちろん、
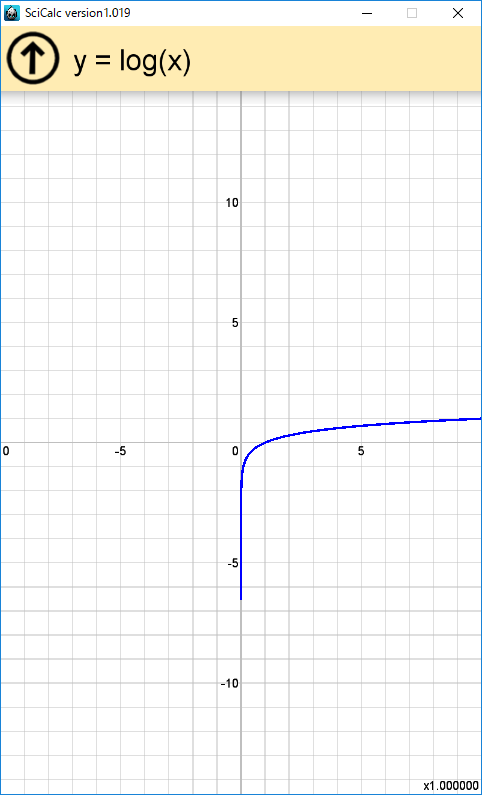
式を自然な数式表示でき、陽関数グラフを描画する機能を実装した。
※ 世界で唯一の○○が□□する関数電卓だよ。
本稿では、その陽関数グラフ描画について述べる。
数式を入力し「=」を押すと計算結果を表示する。
※ 入力された数式(べき乗、ルート)は自然な表記で表示される。

グラフモードに切り替え、変数 x を用いた式(陽関数;y = f(x))を入力し、「=」を押すとグラフを描画。
関数表記には「陽関数」「媒介変数関数」「陰関数」の3種類がある。
「媒介変数関数」「陰関数」のグラフ描画は「陽関数」に比べてグラフ描画の難易度が高い。
描画範囲([X1, X2), [Y1, Y2) )がわかっていれば、陽関数なので、各 x に対応する y はすぐに求めることができる。
単純なアルゴリズムは以下のようになる。
for(x = X1; x < X2; x+=DX) { // 描画範囲内の x について
y = f(x); // y を計算
if( f(x) が有効であれば )
(x, y) をプロット;
}
※ 描画範囲は、画面座標系における座標系原点位置・スケールから決まる。
※ f(x) の計算は、式を構文解析し、演算子の優先順位を考慮して、項・式を評価するだけ。
上記アルゴリズムでは、abs(dy/dx) > 1 の時、グラフが連続しないという問題がある。
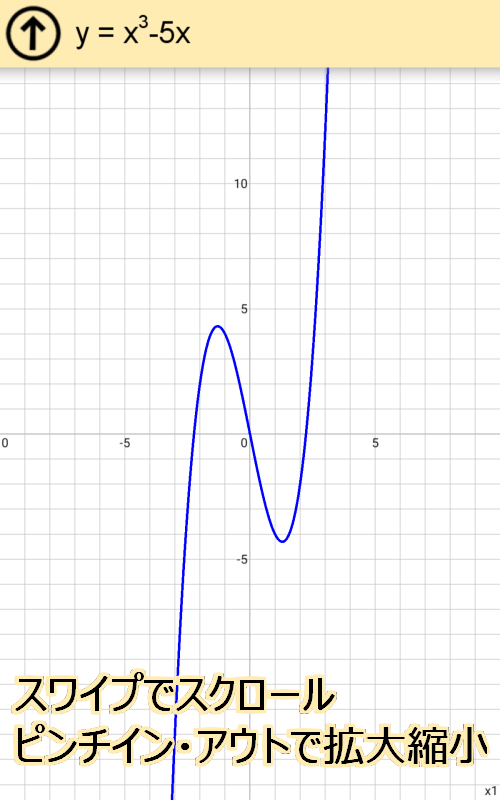
また、√(90-x^2) のように、f(x) が不連続な場合に、端点がプロットされない場合があるという問題もある。
さらに、Android 端末の場合、解像度はまちまちで、X1, X2 は実際の端末により異なるのだが、
cocos2d-x では座標系をすべて共通の論理座標系で指定するのが(おいらの中では)普通で、
それをちゃんと考慮していないとグラフの品質が劣化する。
連続しない問題の解決策として、点を単にプロットするのではなく、それらの間を直線を描画する方法(線形補間)がある。
直前点 = 空;
for(x = X1; x < X2; x+=DX) { // 描画範囲内の x について
y = f(x); // y を計算
if( f(x) が有効 ) {
if( 直前点 != 空 )
直線病が:直前点 - (x, y)
直前点 = (x, y);
} else
直前点 = 空
}
上記のアルゴリズムでグラフは連続するのだが、今度は逆に tan(x) の x = 90度の部分ように連続して欲しくない場合にも、 グラフが連続してしまうという問題が発生する。
端点が描画されないという問題を解決するために「追跡法」を実装した。
x を画面左から順に増やし、有効な点を見つけたら、-x 方向、+x 方向の両方に追跡し、プロットするようにした。
for(x = X1; x < X2; ) { // 描画範囲内の x について
y = f(x); // y を計算
if( f(x) が有効 ) {
-x 方向に対して f(x) が有効である間描画
+x 方向に対して f(x) が有効である間描画
} else
x += DX;
}
abs(dy/dx) > 1 の場合にもグラフを連続させるコード:
// (x, y) から +x 方向に対して f(x) が有効である間描画
while( f(x) が有効 ) {
(x, y) をプロット;
if( abs(dy/dx) <= 1 )
x += DX;
else
x += dx/dy;
}
dy/dx は数式処理により正確に計算することもできるが、現状は ⊿y/⊿x | ⊿x = 0.000001 により計算している。
⊿x はもうっと小さくてもいいかもしれない。最適な⊿x の値は不明。
abs(dy/dx) > 1 の場合は、y をひとつ増やして、それに対応する x を求めればいいのだが、y = f(x) から x = g(y) を求めるのは容易ではない。
√(90-x^2)、tan(x) など、たいていの場合でうまくいくようになった。
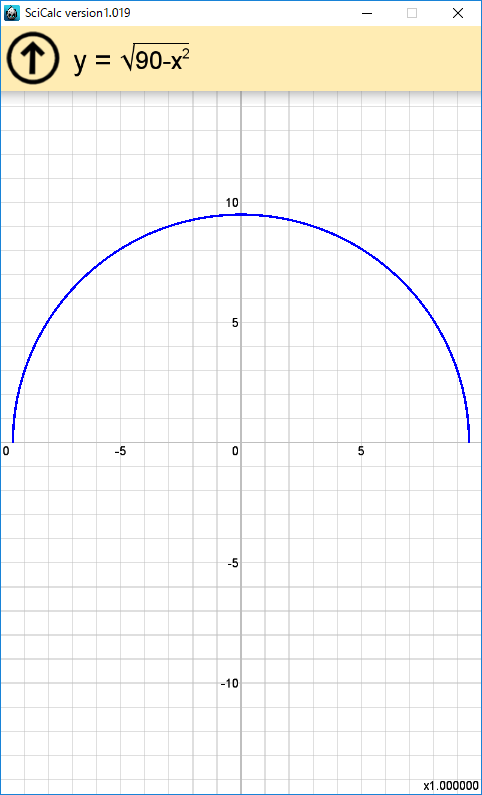
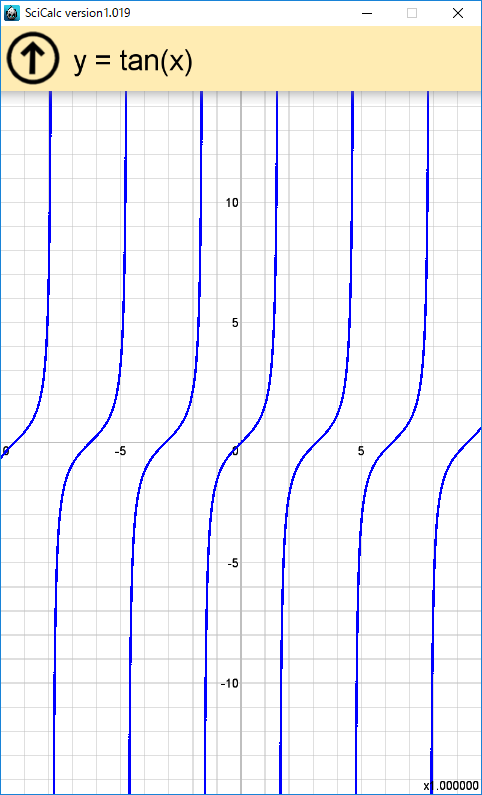
が、dy/dx の絶対値が極端に大きくなると計算誤差により、端点まで描画されなくなることがある。