ニコニコギャモン
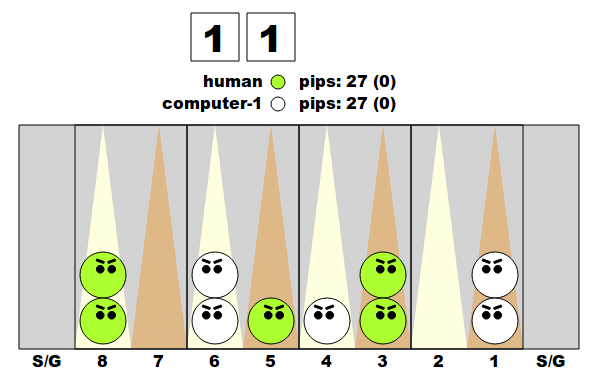
- ニコニコギャモンとはバックギャモンのボードサイズ・石数・サイコロ目の上限を 1/3 にしたものである。
ただし、サイコロの出目を1・2のみにすると、場合の数が3種類になり、ゲームがつまらなくなるので、 サイコロの出目に0を加え、0・1・2としている。 - インナーのポイント数が2個、初期状態でほとんどの石が2個積まれているので、「ニコニコギャモン」と命名した。
※ 1/3 サイズのバックギャモンは「マイクロギャモン」と呼ばれることもある。
状態数の数え上げ・列挙
黒石のみの状態数の数え上げ
- 白黒双方の状態数を数えるのは大変なので、まずは黒石のみの状態数を数える。
- P箇所にN個の石を(それぞれの石を区別せず)置く場合の数を返す関数 PNC(p, n) は以下のように定義できる:
int PNC(int p, // 石を置く場所の数 [1, ∞)
int n) // 石の個数 [0, ∞)
{
if( p == 1 || !n )
return 1;
else
return PNC(p - 1, n) + PNC(p, n - 1);
}
| p\n | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 3 | 6 | 10 | 15 | 21 |
| 4 | 1 | 4 | 10 | 20 | 35 | 56 |
| 5 | 1 | 5 | 15 | 35 | 70 | 126 |
| 6 | 1 | 6 | 21 | 56 | 126 | 252 |
| 7 | 1 | 7 | 28 | 84 | 210 | 462 |
| 8 | 1 | 8 | 36 | 120 | 330 | 792 |
| 9 | 1 | 9 | 45 | 165 | 495 | 1287 |
| 10 | 1 | 10 | 55 | 220 | 715 | 2002 |
状態列挙
- 正確な状態数を求めるには、白黒が同じ箇所にあって配置できない場合を排除しなくてはいけない。
- それを行うには、実際に配置パターンを生成(列挙)し、黒石が無い場所(ただし、スタート・ゴールは重複化) についてのみ白石を配置する状態数を数え上げればよい
- 状態列挙プログラムは以下のように記述できる:
// p 箇所に n 個の石を置くパターン生成
template<typename Container>
bool init_PN(Container &v, int p, int n)
{
if( n < 0 || p <= 0 ) return false;
v.clear();
v << n;
for(int i = 1; i < p; ++i)
v << 0;
return true;
}
template<typename Container>
bool next_PN(Container &v, int vSize)
{
///if( v.size() == 1 ) return false;
// {n0 n1, ...} → {n0-1, n1+1, ...}
// {0, n1, n2,...} → {n1-1, 0, n2+1, ...}
// {0, ... 0, ni, nj,...} → {ni-1, 0, ... 0, nj +1, ...}
// {0, ...n} → return false;
if( v[0] > 0 ) {
--v[0];
++v[1];
} else {
int i = 1;
for(;;) {
if( i == vSize - 1 ) return false;
//if( i == v.size() - 1 ) return false;
if( v[i] != 0 ) break;
++i;
}
++v[i+1];
v[0] = v[i] - 1;
v[i] = 0;
}
return true;
}
// 4箇所に2個の石を置くパターン生成コード:
uchar v[4] = {2, 0, 0, 0}; // 石がすべてゴールにある状態
while( next_PN(v, sizeof(v)) )
qDebug() << v[0] << v[1] << v[2] << v[3];
// 処理結果:
1 1 0 0
0 2 0 0
1 0 1 0
0 1 1 0
0 0 2 0
1 0 0 1
0 1 0 1
0 0 1 1
0 0 0 2
ニコニコギャモン全状態の数え上げ
- 以上で準備が整ったので、ニコニコギャモン全状態の数え上げを行う。アルゴリズムは以下の通りとする
const int nPoint = 8;
const int nStone = 5;
QVector<int> b; // 黒石の状態を表すベクター
init_PN(b, nPoint + 2, nStone); // 10箇所に5個の石を配置する初期配置(石は全部ゴールにある)設定
int sum = 0; // 状態数合計
while( next_PN(b, b.size()) ) { // 次の状態を生成
int ns = b[1]~b[nPoint] の空白数を数える
sum += PNC(ns + 2, nStone) - 1; // ゴール状態を除くために -1
}
// sum に全状態数が格納されている
状態からシーケンシャル番号への変換
- 完全解析を行うには、すべての状態について、すべてのサイコロ目について先読みを行い、加重平均を計算し、期待値を計算しなくてはいけない。
- 計算済みの局面はテーブルに登録し、再度計算しないようにする。
- そのためには、局面の状態から一意のシーケンシャル番号に変換できなくてはいけない。
- シーケンシャル番号は0オリジンとし、前節の next_PN() で生成される順序とする。
- まずは黒石のみの場合のシーケンシャル番号を計算可能にする。
黒石のみの場合のシーケンシャル番号計算
- コンテナ v の v[0]~v[ix] の状態のシーケンシャル番号を計算するには、それ以前の状態の個数を数えればよい。
- したがって、最上位桁の値が [0, v[ix]) の場合の数を数え、桁数を減らしたシーケンシャル番号に加えるとよい。
- コードは以下の様になる。
// {n, 0,...0} を #0 として数える
template<typename Container>
int seqNumber(const Container v,
int ix, // v[0~ix] を参照
int n) // index <= ix の石数
{
Q_ASSERT( ix >= 0 );
if( !n ) return 0; // 0個の石の置き方はひと通りしかない
if( !ix ) return 0; // 最後の桁は自動的に決まる
int sum = 0; // ix の桁が [0, v[ix]) の場合の数を数える
for(int i = 0; i < v[ix]; ++i) {
sum += PNC(ix, n - i);
}
return seqNumber(v, ix - 1, n - v[ix]) + sum;
}
白黒双方の石がある場合のシーケンシャル番号計算
- 白黒双方の石がある場合は、黒のひとつ前状態までの全状態数+白の状態のシーケンシャル番号 を計算すればよい
全期待値計算
- 以上で準備が整ったので、全状態の期待値を計算できる。
- 基本的には、ある状態 S から遷移可能な状態を S1, S2, ... SN とし、それぞれの遷移確率を P1, P2,... PN、 それぞれの期待値を E1, E2, ... EN とすれば、S の期待値は Σ(Pi * Ei) となる。
- 少しだけややこしいのは、局面・サイコロの出目によっては双方パスになる場合があり、 状態Sの期待値を計算するのにその状態Sの期待値が必要になってしまうことである。
- 相互にパスにより遷移する可能性のある状態を Sa, Sb、それぞれの期待値を Ea, Eb とする。
Sa が Sb に遷移(すなわちパス)する確率を P1, Sb が Sb に遷移する確率を P2、
Sa が Sb に遷移しなかった場合の期待値を Ec, Sb が Sa に遷移しなかった場合の期待値を Ed とすると、 以下の関係が成り立つ。
Ea = P1 * Eb + (1 - P1) * Ec Eb = P2 * Ea + (1 - P2) * Edこれを解くと、
Ea = (P1 * (1 - P2) * Ed + (1 - P1) * Ec) / (1 - Ed * P1 * P2)となる。
※ パスが無い場合は P1 = 0 だから、Ea = Ec となる